Toric Geometry of Entropic Regularization
Abstract
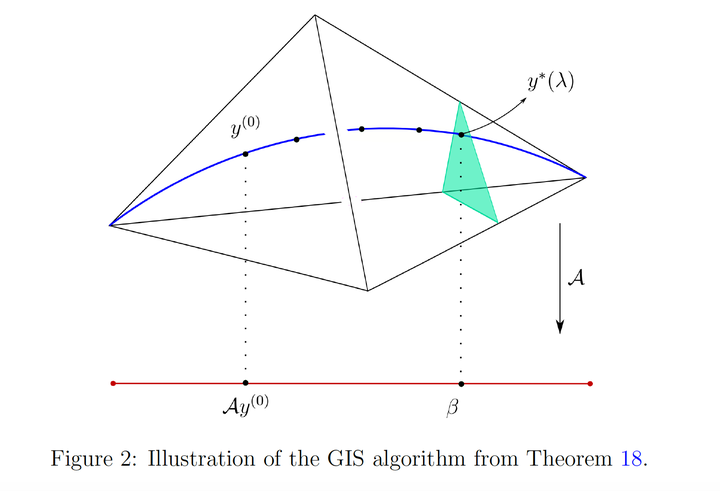
Entropic regularization is a method for large-scale linear programming. Geometrically, one traces intersections of the feasible polytope with scaled toric varieties, starting at the Birch point. We compare this to log-barrier methods, with reciprocal linear spaces, starting at the analytic center. We revisit entropic regularization for unbalanced optimal transport, and we develop the use of optimal conic couplings. We compute the degree of the associated toric variety, and we explore algorithms like iterative scaling.
Type
Publication
MEGA