Faster Unbalanced Optimal Transport: Translation invariant Sinkhorn and 1-D Frank-Wolfe

Abstract

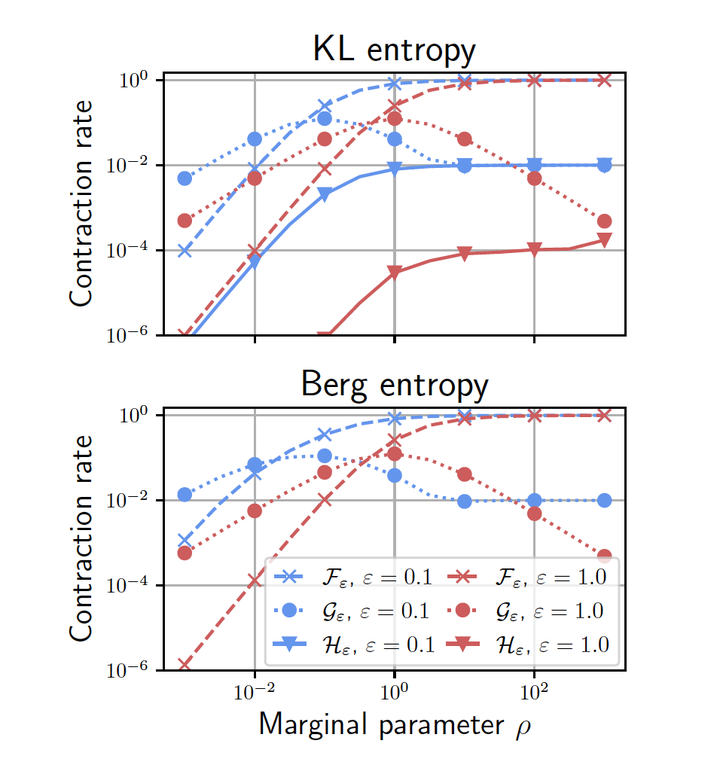
Unbalanced optimal transport (UOT) extends optimal transport (OT) to take into account mass variations to compare distributions. This is crucial to make OT successful in ML applications, making it robust to data normalization and outliers. The baseline algorithm is Sinkhorn, but its convergence speed might be significantly slower for UOT than for OT. In this work, we identify the cause for this deficiency, namely the lack of a global normalization of the iterates, which equivalently corresponds to a translation of the dual OT potentials. Our first contribution leverages this idea to develop an accelerated Sinkhorn algorithm (coined “translation invariant Sinkhorn”) for UOT, bridging the computational gap with OT. Our second contribution focusses on 1-D UOT and proposes a Frank-Wolfe solver applied to this translation invariant formulation. The linear oracle of each steps amounts to solving a 1-D OT problems, resulting in a linear time complexity per iteration. Our last contribution extends this method to the computation of UOT barycenter of 1-D measures. Numerical simulations showcase the convergence speed improvement brought by these three approaches.