Regularity theory and geometry of unbalanced optimal transport

Abstract

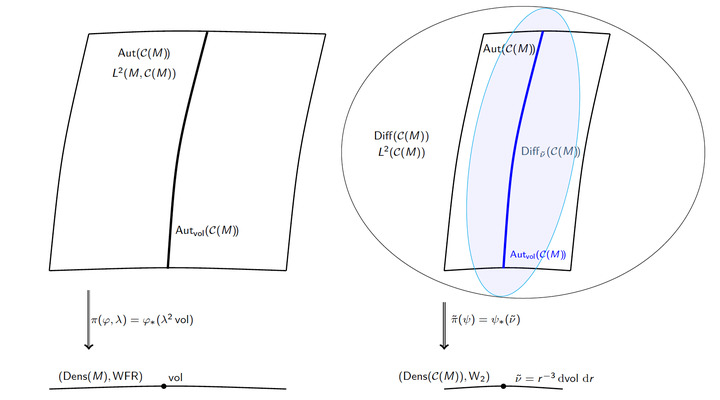
Using the dual formulation only, we show that regularity of unbalanced optimal transport also called entropy-transport inherits from regularity of standard optimal transport.We then provide detailed examples of Riemannian manifolds and costs for which unbalanced optimal transport is regular.Among all entropy-transport formulations, Wasserstein-Fisher-Rao metric, also called Hellinger-Kantorovich, stands out since it admits a dynamic formulation, which extends the Benamou-Brenier formulation of optimal transport.After demonstrating the equivalence between dynamic and static formulations on a closed Riemannian manifold, we prove a polar factorization theorem, similar to the one due to Brenier and Mc-Cann.As a byproduct, we formulate the Monge-Ampère equation associated with Wasserstein-Fisher-Rao metric, which also holds for more general costs.