A geometric Laplace method

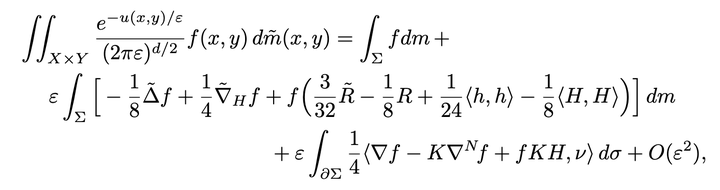
Abstract

A classical tool for approximating integrals is the Laplace method. The first-order, as well as the higher-order Laplace formula is most often written in coordinates without any geometrical interpretation. In this article, motivated by a situation arising, among others, in optimal transport, we give a geometric formulation of the first-order term of the Laplace method. The central tool is the Kim–McCann Riemannian metric which was introduced in the field of optimal transportation. Our main result expresses the first-order term with standard geometric objects such as volume forms, Laplacians, covariant derivatives and scalar curvatures of two different metrics arising naturally in the Kim–McCann framework. Passing by, we give an explicitly quantified version of the Laplace formula, as well as examples of applications.