Gromov-Wasserstein at Scale, Beyond Squared Norms
Abstract
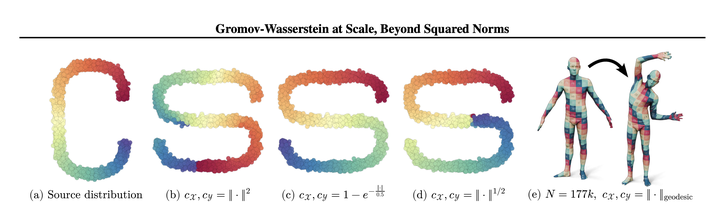
A fundamental challenge in data science is to match disparate point sets with each other. While optimal transport efficiently minimizes point displacements under a bijectivity constraint, it is inherently sensitive to rotations. Conversely, minimizing distortions via the Gromov-Wasserstein (GW) framework addresses this limitation but introduces a non-convex, computationally demanding optimization problem. In this work, we identify a broad class of distortion penalties that reduce to a simple alignment problem within a lifted feature space. Leveraging this insight, we introduce an iterative GW solver with a linear memory footprint and quadratic (rather than cubic) time complexity. Our method is differentiable, comes with strong theoretical guarantees, and scales to hundreds of thousands of points in minutes. This efficiency unlocks a wide range of geometric applications and enables the exploration of the GW energy landscape, whose local minima encode the symmetries of the matching problem.