On the existence of Monge maps for the Gromov-Wasserstein distance

Abstract

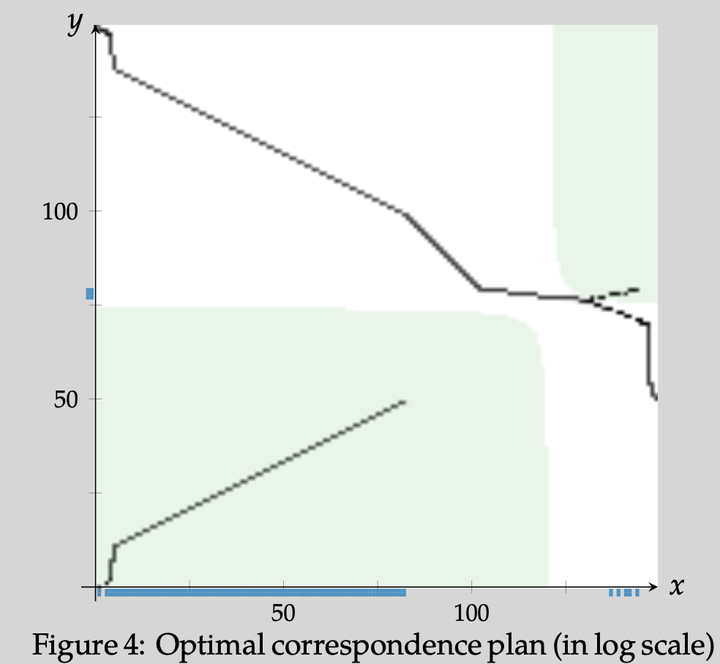
For the L2-Gromov–Wasserstein distance, we study the structure of minimizers in Euclidean spaces for two different costs. The first cost is the scalar product for which we prove that it is always possible to find optimizers as Monge maps and we detail the structure of such optimal maps. The second cost is the squared Euclidean distance for which we show that the worst case scenario is the existence of a map-anti-map structure. Both results are direct and indirect consequences of an existence result on costs that are defined by submersions. In dimension one for the squared distance, we show that a monotone map is optimal in some non-symmetric situations, thereby giving insight on why such a map is often found optimal in numerical experiments. In addition, we show numerical evidence for a negative answer to the existence of a Monge map under the conditions of Brenier s theorem, suggesting that our result cannot be improved in general.