Faster Wasserstein Distance Estimation with the Sinkhorn Divergence

Abstract

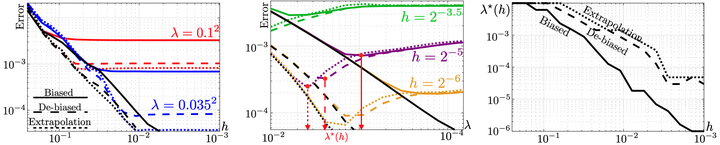
The squared Wasserstein distance is a natural quantity to compare probability distributions in a non-parametric setting. This quantity is usually estimated with the plug-in estimator, defined via a discrete optimal transport problem. It can be solved to ϵ-accuracy by adding an entropic regularization of order ϵ and using for instance Sinkhorn’s algorithm. In this work, we propose instead to estimate it with the Sinkhorn divergence, which is also built on entropic regularization but includes debiasing terms. We show that, for smooth densities, this estimator has a comparable sample complexity but allows higher regularization levels, of order ϵ1/2 , which leads to improved computational complexity bounds and a strong speedup in practice. Our theoretical analysis covers the case of both randomly sampled densities and deterministic discretizations on uniform grids. We also propose and analyze an estimator based on Richardson extrapolation of the Sinkhorn divergence which enjoys improved statistical and computational efficiency guarantees, under a condition on the regularity of the approximation error, which is in particular satisfied for Gaussian densities. We finally demonstrate the efficiency of the proposed estimators with numerical experiments.