Fast Large Deformation Matching with the Energy Distance Kernel
Abstract
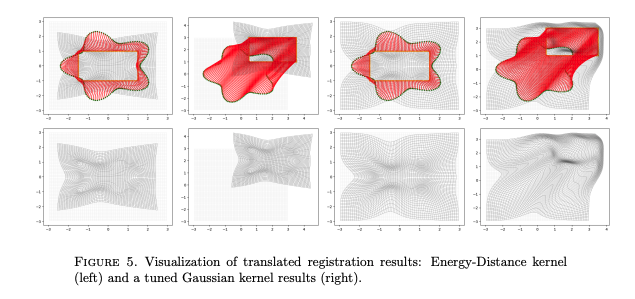
We propose an efficient framework for point cloud and measure registration using bi-Lipschitz homeomorphisms, achieving O(n log n) complexity, where n is the number of points. By leveraging the Energy-Distance (ED) kernel, which can be approximated by its sliced one-dimensional projections, each computable in O(n log n), our method avoids hyperparameter tuning and enables efficient large-scale optimization. The main issue to be solved is the lack of regularity of the ED kernel. To this goal, we introduce two models that regularize the deformations and retain a low computational footprint. The first model relies on TV regularization, while the second model avoids the non-smooth TV regularization at the cost of restricting its use to the space of measures, or cloud of points. Last, we demonstrate the numerical robustness and scalability of our models on synthetic and real data.